BDMO 2012 Junior category problem with solution

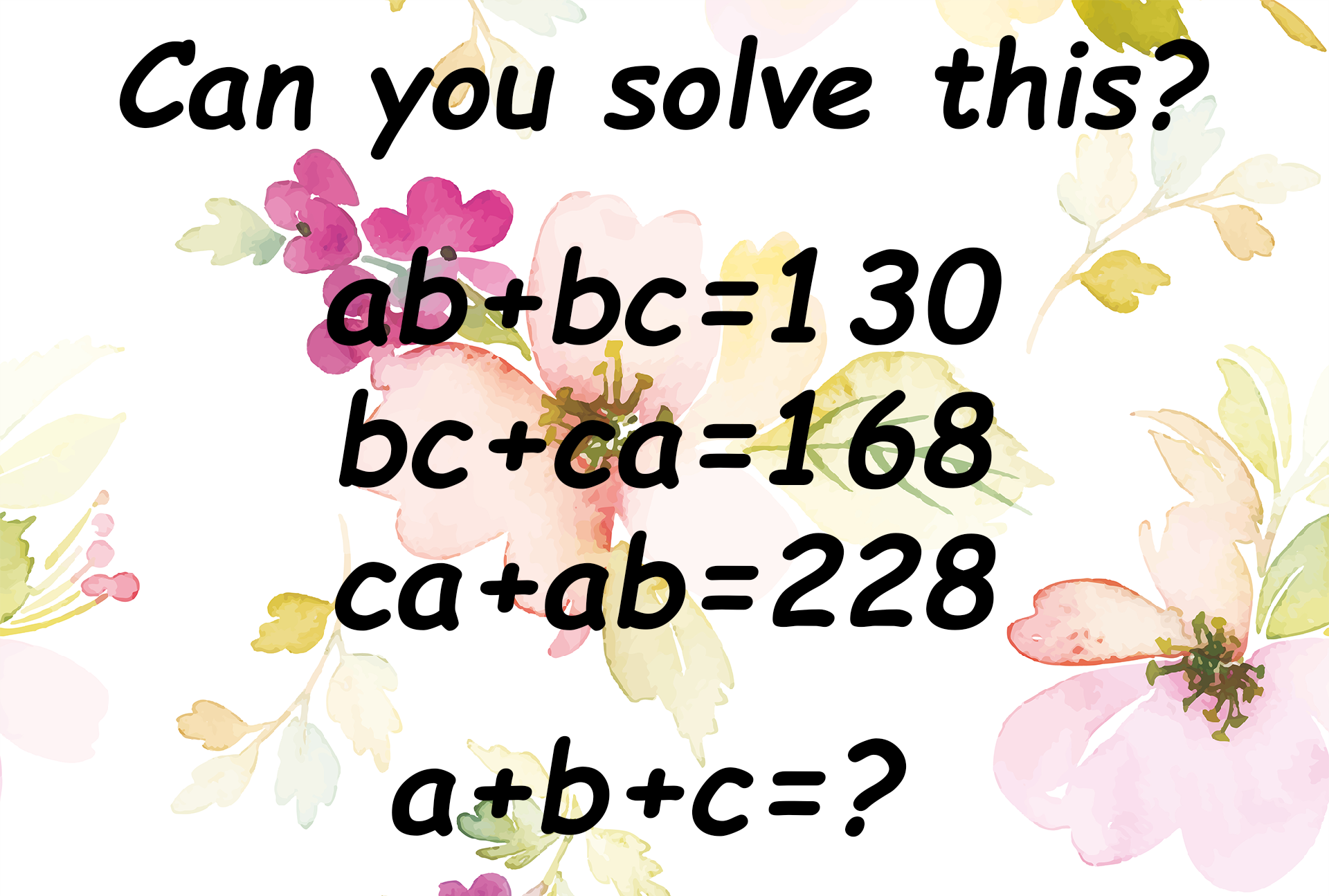
Question:

ab + bc = 130

bc + ca = 168

ca + ab = 228

Then find the value of a+b+c.

Solution:

Given three equations:

ab + bc = 130 ---(i)

bc + ca = 168 ---(ii)

ca + ab = 228 ---(iii)

Adding equations (i), (ii), and (iii), we get:

2ab + 2bc + 2ca = 526

Simplifying the above equation, we get:

ab + bc + ca = 263 ---(iv)

Now, subtracting equation (i) from equation (iv), we get:

ca = 133 ---(v)

Similarly, subtracting equation (ii) from equation (iv), we get:

ab = 95 ---(vi)

And subtracting equation (iii) from equation (iv), we get:

bc = 35 ---(vii)

Dividing equation (v) by equation (vi) and multiplying by equation (vii), we get:

ca / ab x bc = 133 / 95 x 35

Simplifying the above equation, we get:

c^2 = 49

Therefore, c = 7 ---(viii)

Dividing equation (v) by equation (vii) and multiplying by equation (vi), we get:

ca / bc x ab = 133 / 35 x 95

Simplifying the above equation, we get:

a^2 = 361

Therefore, a = 19 ---(ix)

Dividing equation (vii) by equation (v) and multiplying by equation (vi), we get:

bc / ca x ab = 35 / 133 x 95

Simplifying the above equation, we get:

b^2 = 25

Therefore, b = 5 ---(x)

Finally, adding equations (viii), (ix), and (x), we get:

c + a + b = 7 + 19 + 5 = 31

Hence, the value of a+b+c is 31.

In summary, we can solve the given system of equations by adding them up and simplifying, and then using algebraic operations to isolate the values of a, b, and c. By adding these values, we can get the final answer of 31.